| 8.2. Matriz de convolución | ||
|---|---|---|
 |
8. Filtros genéricos |  |
Un dominio de matemáticos. La mayoria de los filtros usan matriz de convolución. Con este filtro, se pueden crear filtros personalizado.
¿Que es una matriz de convolución? Es posible hacerse una idea sin usar las herramientas matemáticas que solo conocen unos pocos. Convolución es el tratamiento de una matriz por otra que se llama “kernel”.
El filtro matriz de convolución usa una primera matriz que es la imagen que será tratada. La imagen es una colección bidimensional de píxeles en coordenada rectágular. El kernel usado depende del efecto deseado.
El GIMP usa matrices 5x5 o 3x3. Consideraremos solo las matrices 3x3, son las más usadas y son suficiente para los efectos deseados. Si todos los valores de un kernel se seleccionan a cero, el sistema la considerará como una matriz 3x3.
El filtro examina, sucesivamente, cada píxel de la imagen. Para cada uno de ellos, que llamaremos “píxeles iniciales”, se multiplica el valor de este píxel y el valor de los 8 circundantes por el valor correspondiente del kernel. Entonces se añade el resultado, y el píxel inicial se regula en este valor resultante final.
Un ejemplo simple:
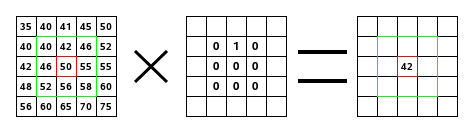
A la izquierda, la imagen de la matriz: cada píxel está marcado con su valor. El píxel inicial tiene un borde rojo. El área de acción del kernel tiene un borde verde. En el medio, el kernel, y a la derecha, el resultado de convolución.
Lo que sucede: el filtro lee sucesivamente, de izquierda a derecha y de arriba a abajo, todos los píxeles del área de acción del kernel. Se multiplica el valor de cada uno de ellos por el valor correspondiente del kernel y se suman los resultados: (100*0)+(50*1)+(50*0)+(100*0) +(100*0)+(100*0)+(100*0)+(100*0)+(100*0)+(100*0) = 50. El píxel inicial asumió el valor 50. Previamente, cuando el píxel inicial tenía el valor=50, tomó el valor 100 del píxel de arriba (el filtro no trabaja sobre la imagen sino sobre una copia) y de esta manera desapareció en el fondo de píxeles a "100". Como resultado gráfico, el píxel inicial se movió un píxel hacia abajo.
Es una matriz kernel de 5x5: el valor se introduce directamente en las cajas.
The result of previous calculation will be divided by this divisor. You will hardly use 1, which lets result unchanged, and 9 or 25 according to matrix size, which gives the average of pixel values.
This value is added to the division result. This is useful if result may be negative. This offset may be negative.
Cuando el píxel inicial está sobre un borde, una parte del kernel se situa fuera de la imagen. Puede decidir que filtro usar:




From left: source image, Extend border, Wrap border, Crop border
This part of kernel is not taken into account.
This part of kernel will study pixels of the opposite border, so pixels disappearing from one side reappear on the other side.
Pixels on borders are not modified, but they are cropped.
Puede seleccionar uno o varios canales con los que trabajará el filtro.
Si esta opción está marcada, el divisor toma el valor resultante de la convolución. Si este resultado es cero (no es posible dividir por cero), se aplica un desplazamiento de 128. Si es negativo (un color negativo no es posible), se aplica un desplazamiento de 255 (se invierte el resultado).
Si esta opción no está marcada, el filtro no tiene en cuenta la transparencia y esto puede producir algunos artefactos cunado se desenfoca.