In this training course, we'll introduce you to the fundamentals of Scheme necessary to use Script-Fu, and then build a handy script that you can add to your toolbox of scripts. The script prompts the user for some text, then creates a new image sized perfectly to the text. We will then enhance the script to allow for a buffer of space around the text. We will conclude with a few suggestions for ways to ramp up your knowledge of Script-Fu.
![[Примітка]](images/note.png)
|
Примітка |
|---|---|
|
This section was adapted from a tutorial written for the GIMP 1 User Manual by Mike Terry. |
Scheme is a dialect of the Lisp family of programming languages. GIMP uses TinyScheme, which is a lightweight interpreter of a subset of the so-called R5RS standard.
Перше, що слід вивчити, це:
Усі інструкції у Scheme записують у дужках ().
Друге, що слід знати, це:
The function name/operator is always the first item in the parentheses, and the rest of the items are parameters to the function.
However, not everything enclosed in parentheses is a function — they can also be items in a list — but we'll get to that later. This notation is referred to as prefix notation, because the function prefixes everything else. If you're familiar with postfix notation, or own a calculator that uses Reverse Polish Notation (such as most HP calculators), you should have no problem adapting to formulating expressions in Scheme.
The third thing to understand is that:
Mathematical operators are also considered functions, and thus are listed first when writing mathematical expressions.
This follows logically from the prefix notation that we just mentioned.
Here are some quick examples illustrating the differences between prefix, infix, and postfix notations. We'll add a 1 and 23 together:
-
Prefix notation:
+ 1 23(the way Scheme will want it) -
Infix notation:
1 + 23(the way we «normally» write it) -
Postfix notation:
1 23 +(the way many HP calculators will want it)
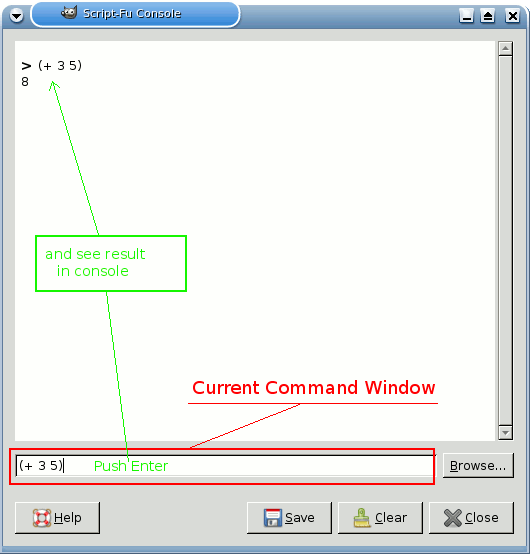
In GIMP, select → → → from the main menu. This will start up the Script-Fu Console window, which allows us to work interactively in Scheme.
At the bottom of this window is a text entry field for commands. Here, we can test out simple Scheme commands interactively. Let's start out easy, and add some numbers:
(+ 3 5)
Typing this in and hitting Enter yields the expected answer of 8 in the center window.
The «+» function can take more arguments, so we can add more than one number:
(+ 3 5 6)
This also yields the expected answer of 14.
So far, so good — we type in a Scheme statement and it's executed immediately in the Script-Fu Console window. Now for a word of caution…
If you're like me, you're used to being able to use extra parentheses whenever you want to — like when you're typing a complex mathematical equation and you want to separate the parts by parentheses to make it clearer when you read it. In Scheme, you have to be careful and not insert these extra parentheses incorrectly. For example, say we wanted to add 3 to the result of adding 5 and 6 together:
3 + (5 + 6) + 7 = ?
Knowing that the + operator can take a list of numbers to add, you might be tempted to convert the above to the following:
(+ 3 (5 6) 7)
However, this is incorrect — remember, every statement in Scheme starts and ends with parens, so the Scheme interpreter will think that you're trying to call a function named «5» in the second group of parens, rather than summing those numbers before adding them to 3.
The correct way to write the above statement would be:
(+ 3 (+ 5 6) 7)
If you are familiar with other programming languages, like C/C++, Perl or Java, you know that you don't need white space around mathematical operators to properly form an expression:
3+5, 3 +5, 3+ 5
These are all accepted by C/C++, Perl and Java compilers. However, the same is not true for Scheme. You must have a space after a mathematical operator (or any other function name or operator) in Scheme for it to be correctly interpreted by the Scheme interpreter.
Practice a bit with simple mathematical equations in the Script-Fu Console until you're totally comfortable with these initial concepts.