Filters Randen zoeken naar randen tussen verschillende kleuren en kunnen zo omtrekken van objecten detecteren.

Ze worden gebruikt om selecties te maken en voor vele artistieke doeleinden.

Deze categorie beschrijft de volgende filters:

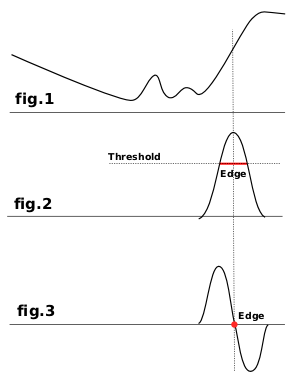
De meeste van hen zijn gebaseerd op methoden voor het berekenen van kleurverlopen en geven dikke lijnen voor de randen. Bekijk afb.1 die de variaties voor de kleurintensiteit weergeeft. Aan de linkerkant staat een traag kleurverloop dat geen rand is. Aan de rechterkant een snelle variatie die een rand is. Dus, laten we het kleurverloop, de snelheid van de variatie, van deze rand berekenen, d.i. de eerste afgeleide (afb.2). We zullen moeten beslissen dat een rand is gedetecteerd als het kleurverloop meer is dan een drempelwaarde (de exacte rand ligt aan de bovenzijde van de curve, maar die bovenzijde varieert met de randen). In de meeste gevallen is de drempel onder en boven de rand dik.

Het detecteren van randen Laplacian gebruikt de tweede afgeleide (afb.3). De bovenzijde van de curve staat nu op nul en is duidelijk geïdentificeerd. Dat is waarom het filter Laplace een dunne rand rendert, slechts een beeldpunt breed. Maar deze afgeleide geeft verscheidene nullen die overeenkomen met kleine rimpels, wat resulteert in valse randen.

Enig vervagen voor het toepassen van filters voor randen is vaak nodig: het maakt kleine rimpels in het signaal vlak en voorkomt zo valse randen.