| 9.2. Convolutiematrix | ||
|---|---|---|
|
9. Filters Algemeen |  |
| 9.2. Convolutiematrix | ||
|---|---|---|
|
|
9. Filters Algemeen | |
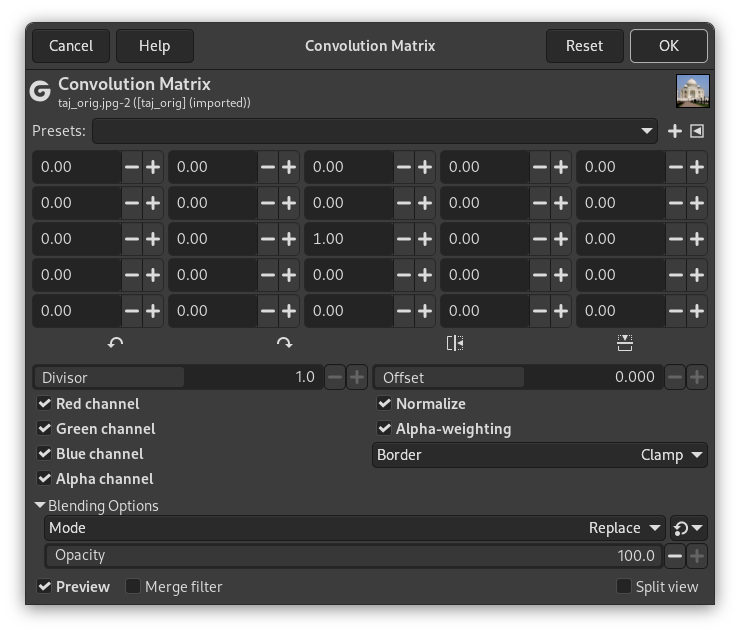
Dit is het domein voor een wiskundige. De meeste filters gebruiken een convolutiematrix. Met het filter Convolutiematrix, als u dat leuk vindt, kunt u een aangepast filter maken
Wat is een convolutiematrix? Het is mogelijk er een ruw idee van te krijgen, zonder wiskundige gereedschappen te gebruiken die slechts weinigen kennen. Convolutie is de behandeling van een matrix door een andere die “kernel” wordt genoemd.
Het filter Convolutiematrix gebruikt een eerste matrix, wat de afbeelding is die moet worden behandeld. De afbeelding is een bi-dimensionale collectie pixels binnen rechthoekige coördinaten. De gebruikte kernel is afhankelijk van het effect dat u wilt bereiken.
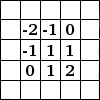
GIMP gebruikt matrices 5×5 of 3×3. We zullen alleen matrices 3×3 behandelen, zij worden het meest gebruikt en zij zijn voldoende voor alle effecten die u zou willen bereiken. Als alle grenswaarden van een kernel zijn ingesteld op nul, dan zal het systeem het beschouwen als een 3x3 matrix.
Het filter beoordeelt achtereenvolgens elke pixel van de afbeelding. Voor elk ervan, wat we de “initiële pixel” zullen noemen, vermenigvuldigt het de waarde van deze pixel en de waarden van de 8 omliggende pixels met de corresponderende waarde van de kernel. Dan worden de resultaten opgeteld en de initiële pixel wordt ingesteld op deze uiteindelijke waarde.
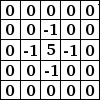
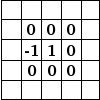
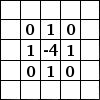
Een eenvoudig voorbeeld:
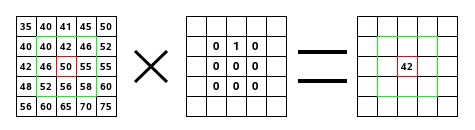
Aan de linkerkant staat de afbeeldingsmatrix: elke pixel is gemarkeerd met zijn waarde. De initiële pixel heeft een rode rand. Het actiegebied van de kernel heeft een groene rand. In het midden staat de kernel en, aan de rechterkant, het resultaat van de convolutie
Hier is wat er gebeurde: het filter las achtereenvolgens, van links naar rechts en van boven naar beneden, alle pixels van het actiegebied van de kernel. Het vermenigvuldigde de waarde van elk ervan met de corresponderende waarde uit de kernel, en telde de resultaten daarbij op. De initiële pixel is 42 geworden: (40*0)+(42*1)+(46*0) + (46*0)+(50*0)+(55*0) + (52*0)+(56*0)+(58*0) = 42. (het filter werkt niet op de afbeelding maar op een kopie ervan). Als grafisch resultaat is de initiële pixel een pixel naar beneden verplaatst.
![[Opmerking]](images/note.png)
|
Opmerking |
|---|---|
|
Deze opties staan beschreven in Paragraaf 2, “Algemene eigenschappen”. |
Dit is de 5×5 kernelmatrix: u voert de gewenste waarden direct in de vakken in.
Het resultaat van de eerdere berekening zal worden gedeeld door deze deler. U zult meest waarschijnlijk niets anders gebruiken dan 1, wat de resultaten onveranderd laat, en 9 of 25 overeenkomstig de grootte van de matrix, wat het gemiddelde van de waarden van de pixels geeft. De deler kan alleen worden gewijzigd als Normaliseren is uitgeschakeld.
Deze waarde wordt opgeteld bij het resultaat van de deling. Dat is nuttig als het resultaat negatief zou kunnen zijn. Deze verschuiving mag negatief zijn. Het kan alleen worden gewijzigd als Normaliseren is uitgeschakeld.
Hier kunt u selecteren welke kanalen het filter zou moeten wijzigen.
Als deze optie is geselecteerd, neemt de deler het resultaat over van de waarde van de convolutie. Als dit resultaat gelijk is aan nul (het is niet mogelijk om door nul te delen), dan wordt een verschuiving van 128 toegepast. Als dit negatief is (een negatieve kleur is niet mogelijk), wordt een verschuiving van 255 toegepast (inverteert het resultaat).
Als deze optie niet is geselecteerd, houd het filter geen rekening met transparantie en dat zou enige artefacten kunnen veroorzaken bij blurren.
Als de initiële pixel op een rand ligt, zal een deel van de kernel buiten de afbeelding liggen. U moet bepalen wat het filter zou moeten doen:
Met dit deel van de kernel wordt geen rekening gehouden.
Pixels op randen worden niet aangepast, zij worden bijgesneden.
Dit deel van de kernel zal worden beïnvloed door pixels van de tegenoverliggende rand, pixels verdwijnen dus van de ene rand en verschijnen opnieuw aan de andere kant.
Pixels op randen worden naar zwart gewijzigd.
Pixels op randen worden naar wit gewijzigd.
Ontwerpen van kernels is gebaseerd op wiskunde op hoog niveau. Reeds gemaakte kernels zijn te vinden op het web. Hier zijn enkele voorbeelden:
