| 9.2. Foldningsmatrix | ||
|---|---|---|
|
9. Generelle filtre |  |
| 9.2. Foldningsmatrix | ||
|---|---|---|
|
|
9. Generelle filtre | |
Det her er en matematikers domæne. De fleste filtre bruger foldningsmatrix. Med filteret Foldningsmatrix kan du lave et brugerdefineret filter, hvis du får lyst til det.
Hvad er en foldningsmatrix? Det er muligt at få en idé om det uden at bruge matematiske værktøjer, som kun de færreste kender. Foldning er behandlingen af en matrix med en anden, som kaldes “kernen”.
Filteret foldningsmatrix bruger en første matrix, som er det billede, der skal behandles. Billedet er en todimensional samling af pixels i rektangulære koordinater. Den anvendte kerne afhænger af den effekt, du ønsker.
GIMP bruger 5×5- eller 3×3-matricer. Vi vil kun se på 3×3-matricer, da de er de mest brugte, og de er nok til alle de effekter, du ønsker. Hvis alle kantværdier i en kerne er sat til nul, vil systemet betragte den som en 3×3-matrix.
Filteret undersøger successivt hver pixel i billedet. For hver af dem, som vi vil kalde “den oprindelige pixel”, multiplicerer det værdien af denne pixel og værdierne af de 8 omkringliggende pixels med kernens tilsvarende værdi. Derefter lægger den resultaterne sammen, og begyndelsespixlens værdi sættes til denne endelige resultatværdi.
Et simpelt eksempel:
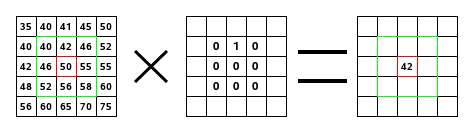
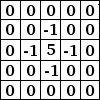
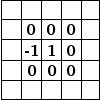
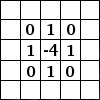
Til venstre ses billedmatrixen: Hver pixel er markeret med sin værdi. Den oprindelige pixel har en rød kant. Kernens aktionsområde har en grøn kant. I midten er kernen, og til højre er foldningsresultatet.
Her er, hvad der skete: Filteret læste successivt, fra venstre mod højre og fra top til bund, alle pixels i kernens aktionsområde. Det multiplicerede værdien af hver af dem med kernens tilsvarende værdi og lagde resultaterne sammen. Den oprindelige pixel er blevet 42: (40*0)+(42*1)+(46*0) + (46*0)+(50*0)+(55*0) + (52*0)+(56*0)+(58*0) = 42 (filteret virker ikke på billedet, men på en kopi). Som et grafisk resultat er den oprindelige pixel flyttet en pixel nedad.
![[Bemærk]](images/note.png)
|
Bemærk |
|---|---|
|
Disse indstillinger er beskrevet i Afsnit 2, “Fælles funktioner”. |
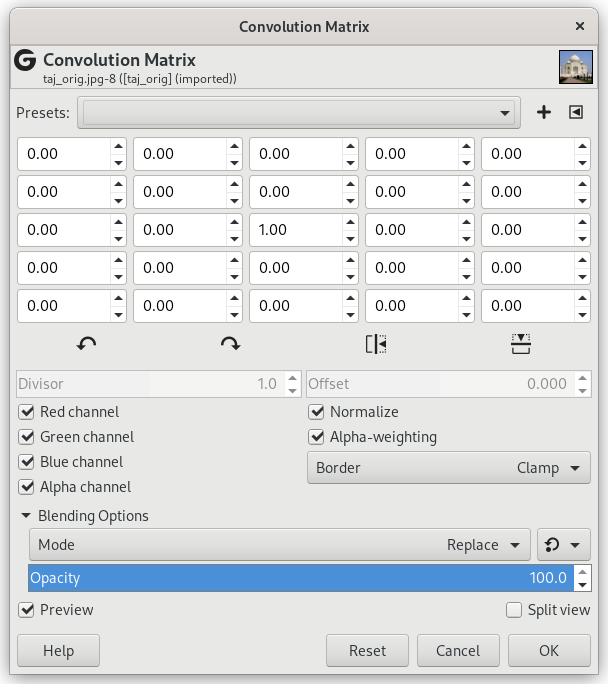
Dette er 5×5-kernematrixen: Du indtaster de ønskede værdier direkte i felterne.
Resultatet af den foregående beregning divideres med denne divisor. Du vil næppe bruge andet end 1, som efterlader resultaterne uændrede, og 9 eller 25 afhængigt af matrixstørrelsen, som giver gennemsnittet af pixelværdierne. Divisoren kan kun ændres, når Normalisér ikke er markeret.
Denne værdi lægges til divisionsresultatet. Dette er nyttigt, hvis resultatet kan være negativt. Denne forskydning kan være negativ. Den kan kun ændres, når Normalisér ikke er markeret.
Her vælges hvilke kanaler, filteret skal ændre.
Hvis denne indstilling er markeret, tager divisoren resultatværdien af foldningen. Hvis dette resultat er lig med nul (det er ikke muligt at dividere med nul), anvendes en forskydning på 128. Hvis den er negativ (en negativ farve er ikke mulig), anvendes en forskydning på 255 (inverterer resultatet).
Hvis denne indstilling ikke er markeret, tager filteret ikke højde for gennemsigtighed, og det kan føre til nogle artefakter ved sløring.
Når den oprindelige pixel er på en kant, er en del af kernen uden for billedet. Du er nødt til at beslutte, hvad filteret skal gøre:
Denne del af kernen tages ikke i betragtning.
Pixels på kanterne ændres ikke, men de beskæres.
Denne del af kernen vil blive påvirket af pixels fra den modsatte kant, så pixels, der forsvinder fra den ene side, dukker op igen på den anden side.
Pixels på kanterne gøres sorte.
Pixels på kanterne gøres hvide.
