| 9.2. Konturutjamningsmatrise | ||
|---|---|---|
|
9. Generelle filter |  |
| 9.2. Konturutjamningsmatrise | ||
|---|---|---|
|
|
9. Generelle filter | |
Dette filteret vert mest brukt for å laga og å prøva ut eigne filter. Når du brukar filteret, set du opp ei konvolusjonsmatrise, den såkalla kjernen, som så vert brukt på biletet. Dette er eigentleg høgare matematikk, men forklaringa nedanfor skulle gje eit godt grunnlag for å ta i bruk filteret sjølv om du ikkje er matematikar. Skulle du ha behov for meir matematikk, kan du prøva Wikipedia eller andre oppslagsverk. Sidan mange av filtra i GIMP er laga med same matematikken, bør du ikkje verta forundra om du kjenner igjen nokre av sekvensane.
Kva i all verda er eigentleg ei konturutjamningsmatrise? For å ta det siste først. Ei matrise er i denne samanhengen eit mønster sett opp i tabellform. Konturutjamning, eller betre: konvolusjon, er å kombinera to matrise på ein eller annan måte og overføre resultatet til den første matrisa.
I konturutjamningsfilteret vert biletet oppfatta som den første matrisa, ei todimensjonal samling av pikslar set opp i rektangulære ruter. Den andre matrisa, den såkalla kjernematrisa vert sett opp av deg. Innhaldet i denne matrisa er avhengig av kva effekt du ønskjer av filteret.
GIMP brukar 5 × 5 eller 3 × 3 matriser. Her skal me konsentrera oss om 3 × 3 matriser sidan desse er mest brukte. Dessutan kan du bruka desse matrisene til alle ønskte effektar. Dersom alle rammeverdiane i ei kjernematrise er sett til null, vil systemet oppfatta dette som ei 3 × 3 matrise.
Filteret analyserer kvar enkelt piksel i biletet etter tur. Den pikselen som for tida vert analysert, kallar vi her for initialpikselen. Verdien av denne og verdiane av dei 8 omkringliggjande pikslane vert multipliserte med den tilsvarande verdien i kjernen. Den nye verdien til initialpikselen vert sluttverdien.
Eit enkelt eksempel:
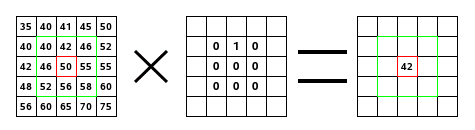
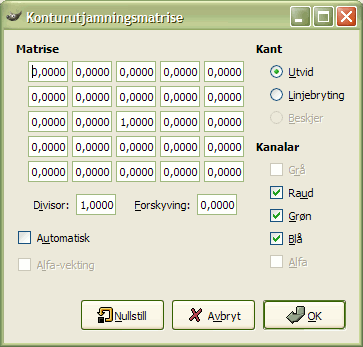
Til venstre er matrisa for biletet: Kvar piksel er merkt med verdien han har. Initialpikselen er i sentrum og er markert med ein raud kant. Området som vert påverka av kjernematrisa er markert med ei grøn ramme. I midten kjernen og biletet til høgre det ferdige resultatet.
Her er kva som skjer: Filteret les piksel for piksel frå venstre mot høgre og frå topp til botn gjennom heile området som vert påverka av kjernen. Verdien for kvar piksel vert multiplisert med tilsvarande verdi i kjernen og resultatet vert lagt til dei andre verdiane slik: (40 · 0) + (42 · 1) + (46 · 0) + (46 · 0) + (50 · 0) + (55 · 0) + (52 × 0) + (52 · 0) + (56 · 0) + (58 · 0) = 42. Den nye verdien for initialpikselen vert i eksemplet altså 42.
![[Notat]](images/note.png)
|
Notat |
|---|---|
|
Desse innstillingane er omtalte i Del 2, «Felles eigenskapar». |
Dette er den 5 × 5 kjernematrisa: Du skriv dei ønskte verdiane direkte i kvar rute.
Resultatet av den førre kalkulasjonen vert dividert med dette talet. Du vil svært sjeldan bruka noko anna enn 1, som gjer at resultatet ikkje vert endra. Verdiane 9 eller 25, avhengig av matrisestorleiken, vil gje gjennomsnittet av pikselverdiane. Divisoren kan endrast berre når det ikkje er merkt av for «Normaliser».
Denne verdien vert lagt til resultatet av divisjonen for å unngå negativt resultat. Forskyvinga kan derimot vere negativ. Dette kan endrast berre når det ikkje er merkt av for «Normaliser».
Du bestemmer her kva kanalar filteret skal verka på.
Når det er merkt av for dette valet, vert divisor sett automatisk. Dersom resultatet vert 0 (det er ikkje råd å dele med 0) vert det lagt til 128. Sidan negative fargeverdiar ikkje finst, vil eit negativt resultat verta invertert (dvs. det vert lagt til 255).
Dersom det ikkje er avmerkt for dette valet, vert ein eventuell alfakanal i biletet ikkje rekna med. Dette kan føra til ein del merkelege effektar dersom biletet vert sløra.
Når filteret arbeider på biletkanten, vil delar av kjernen vera utanfor biletet. Du må her bestemma kva filteret skal gjera med dette:
Denne delen av kjernen vert ikkje rekna med.
Pikslane ved kanten vert ikkje endra, men klipte.
Denne delen av kjernen vert påverka av pikslane på den motsette kanten av biletet. Pikslar som forsvinn frå ei side dukkar opp på den andre sida av biletet.
Pikslane ved kanten vert endra til svarte.
Pikslane ved kanten er endra til kvite.
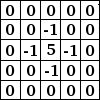
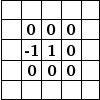
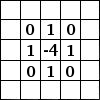
Oppsettet av ei kjerne bygger eigentleg på avansert matematikk, men du kan gjerne prøve deg fram, eller leite opp ferdige kjerner på Internett. Her er nokre få eksempel:
