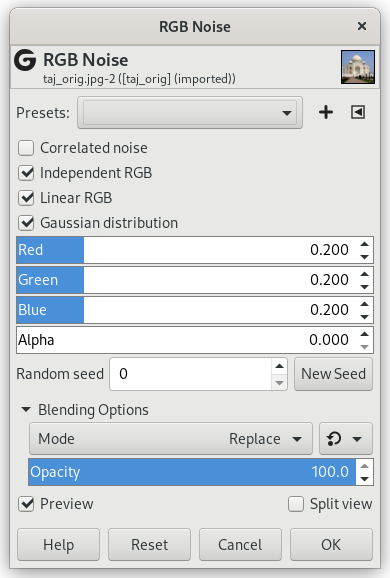
The RGB Noise filter adds a normally distributed noise to a layer or a selection. It uses the RGB color model to produce the noise (noise is added to red, green and blue values of each pixel). A normal distribution means, that only slight noise is added to the most pixels in the affected area, while less pixels are affected by more extreme values. (If you apply this filter to an image filled with a solid gray color and then look at its histogram, you will see a classic bell-shaped Gaussian curve.)
The result is very naturally looking noise.
- Presets, „Input Type“, Clipping, Blending Options, Preview, Merge filter, Split view
-
![[Pastaba]](images/note.png)
Pastaba These options are described in Skyrius 2, „Common Features“.
- Correlated noise
-
Noise may be additive (uncorrelated) or multiplicative (correlated - also known as speckle noise). When checked, every channel value is multiplied by a normal distributed value. So the noise depends on the channel values: a greater channel value leads to more noise, while dark colors (small values) tend to remain dark.
- Independent RGB
-
When this radio button is checked, you can move each RGB slider separately. Otherwise, the sliders R, G and B will be replaced by a single slider Value. The same relative noise will then be added to all channels in each pixel, so the hue of pixels does not change much.
- Linear RGB
-
Operate on linearized RGB color data.
- Gaussian distribution
-
Use a gaussian noise distribution. When unchecked, a linear noise distribution is used instead.
- Red, Green, Blue, Alpha
-
These slidebars and adjacent input boxes allow to set noise level (0.00 - 1.00) in each channel.
The value set by these sliders actually determine the standard deviation of the normal distribution of applied noise. The used standard deviation is a half of the set value (where 1 is the distance between the lowest and highest possible value in a channel).
- Random seed, New Seed
-
This option controls the randomness of the filter. The Random seed box lets you manually enter a seed for the randomization algorithm used. You can also generate a random seed by pressing the button. If the same random seed is used in the same situation, the filter produces exactly the same results. A different random seed produces different results.